Lineare oder logarithmische Chartdarstellung

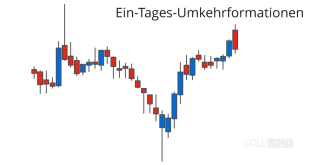
Für eine optische Darstellung von großen Datenmengen und deren Auswertung werden Charts verwendet. An den Finanzmärkten wird am häufigsten die zweidimensionale Chartdarstellung mit einer horizontalen Zeitachse X und einer vertikalen Kursachse Y verwendet. Die Chartarten können aber vielfältig sein. So werden in den Medien meist Liniencharts gezeigt die hervorragend als Langfristbeobachtung nützlich sind. Börsianer nutzen häufig Balkencharts oder Kerzencharts auch als Candlestick-Charts bekannt. Unter Wissenschaftlern ist eine Aussage von zukünftigen Kursverläufen äußerst umstritten. Unumstritten ist die Tatsache, dass sich in den Chartmustern Formationen bilden, die mit eine gewissen Wahrscheinlichkeit auch in Zukunft Bestand haben.

Ob Börsenkurse steigen oder fallen ist doch Zufall.
Für Börsianer ist eine einfache Betrachtung der Kursverläufen unerlässlich. Die Technik der Auswertung von Börsencharts ist die Charttechnik oder Chartanalyse. Mit der Chartanalyse lässt sich der richtige Kauf- oder Verkaufszeitpunkt unter dem Aspekt einer Risikominimierung mit einer bestimmten Wahrscheinlichkeit ermitteln.

Lineare oder logarithmische Chartdarstellung für Kurse
Charts können unterschiedlich dargestellt werden, hier unterscheidet sich die gängige lineare oder arithmetische von der logarithmischen Chartdarstellung. Das Besondere bei der logarithmischen auch halblogarithmische Darstellung genannt ist die Y-Achse (Kursskala oder Kursachse). Halblogarithmisch da nur die Y-Achse logarithmisch skaliert ist. Bei einer logarithmischen Skalierung werden Kursbewegungen verhältnismäßiger dargestellt, gerade bei langen Zeitintervallen (Langfristcharts) oder bei Charts einer hohen Volatilität. Bei der arithmetischen Skalierung, die auch als lineare Skalierung bezeichnet wird, stehen gleiche Abstände auf der Kursskala auch für die gleichen Kurseinheiten. Bei einer logarithmischen Skalierung stehen die gleichen Abstände auf einer Kursskala für prozentual gleich bleibende Kursveränderungen. So schlagen sich die Gewinne und Verluste bei einer logarithmischen Skalierung im ähnlichen Ausmaß nieder, wie diese auch den Wert im Depot beeinträchtigen. So haben diese, wenn die Kursschwankungen niedrig ist und nur über einen kurzen Zeitraum betrachtet werden, nur sehr geringe Auswirkungen auf die unterschiedlichen Skalierungen. Werden die Kursbewegungen jedoch über einen längeren Zeitraum betrachtet bei hoher Veränderung im Kursniveau, so sind die Unterschiede in der Darstellung erheblich.

Logarithmische Chartdarstellung am Beispiel des Goldpreises
Die logarithmische Chartdarstellung trägt der Tatsache Rechnung, dass sich Börsenkurse in einer prozentualen Spanne bewegen unabhängig davon auf welchen Preisniveau sich der Wert befindet. So bewegt sich der Goldpreis im Jahr 2004 in einer Spanne zwischen 370 und 460 USD im Schnitt um 5 USD am Tag oder 1,2%. Im Jahr 2012 bewegte sich der Goldpreis auf ein Preisniveau von 1540 bis 1800 USD im Schnitt am Tag um etwa 22 USD oder 1,3%. Die logarithmische Chartdarstellung wird aus diesem Grund hauptsächlich von Börsianern genutzt, da die prozentuale Darstellung der Kursschwankungen sehr wichtig ist.

Chart-Softwareprogramme haben in der Regel die optionale Umstellmöglichkeit zwischen der linearen und der logarithmischen Darstellungsart. Bei einer linearen Darstellung werden auf der vertikalen Kursskala gleiche Abstände zwischen den einzelnen Einteilungen in Punkten angezeigt. So ist der Abstand zwischen den Werten immer gleich groß, was den Nachteil mit sich bringt, dass meistens übersehen wird, dass die erste Kurssteigerung hundert Prozent ist und die Zweite nur eine geringere Veränderung mit sich bringt. Anders ist es bei der logarithmischen Darstellung, denn hier stehen gleiche vertikale Abstände auch für prozentual identische Abstände bei den Kursen. Und so entspricht die Kursbewegung von zehn auf zwanzig der gleichen Wegstrecke wie bei einem Anstieg von 20 auf 40. Dieser Unterschied kann auch sehr bedeutend sein, wenn es um die Trendlinien geht.

Beim der Betrachten des Aktienkurses der Infineon-Aktie im Langfristchart werden die Unterschiede der Skalierung besonders deutlich. So kann man den Einbruch im Jahre 2009 auf unter 0,5 Euro in der arithmetischen Skalierung, anders als in der logarithmischen fast nicht erkennen.